Featured image of post BUAA-OO-Unit1
BUAA-OO

BUAA-OO-Unit1

表达式化简

BUAA-OO-Unit1总结

三次迭代回顾

HW1

本次作业需要完成的任务为：读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的单变量表达式，输出恒等变形展开所有括号后的表达式。

在本次作业中，展开所有括号的定义是：对原输入表达式 EE 做恒等变形，得到新表达式 E′E′，且 E′E′ 中不含有字符 ( 、 )和空白字符 。

HW2

本次作业中需要完成的任务为：读入自定义递推函数的定义以及一个包含幂函数、三角函数、自定义递推函数调用的表达式，输出恒等变形展开所有括号后的表达式。

在本次作业中，展开所有括号的定义是：对原输入表达式 EE 做恒等变形，得到新表达式 E′E′。其中，E′E′ 中不再含有自定义递推函数，且只包含必要的括号（必要括号的定义见公测说明-正确性判定）。

HW3

本次作业中需要完成的任务为：读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用、求导算子的表达式，输出恒等变形展开所有括号后的表达式。

在本次作业中，展开所有括号的定义是：对原输入表达式 EE 做恒等变形，得到新表达式 E′E′。其中，E′E′ 中不再含有自定义函数，不再含有求导算子，且只包含必要的括号（必要括号的定义见公测说明-正确性判定）。

在本次作业中，自定义函数 指自定义递推函数和自定义普通函数。

设计思路

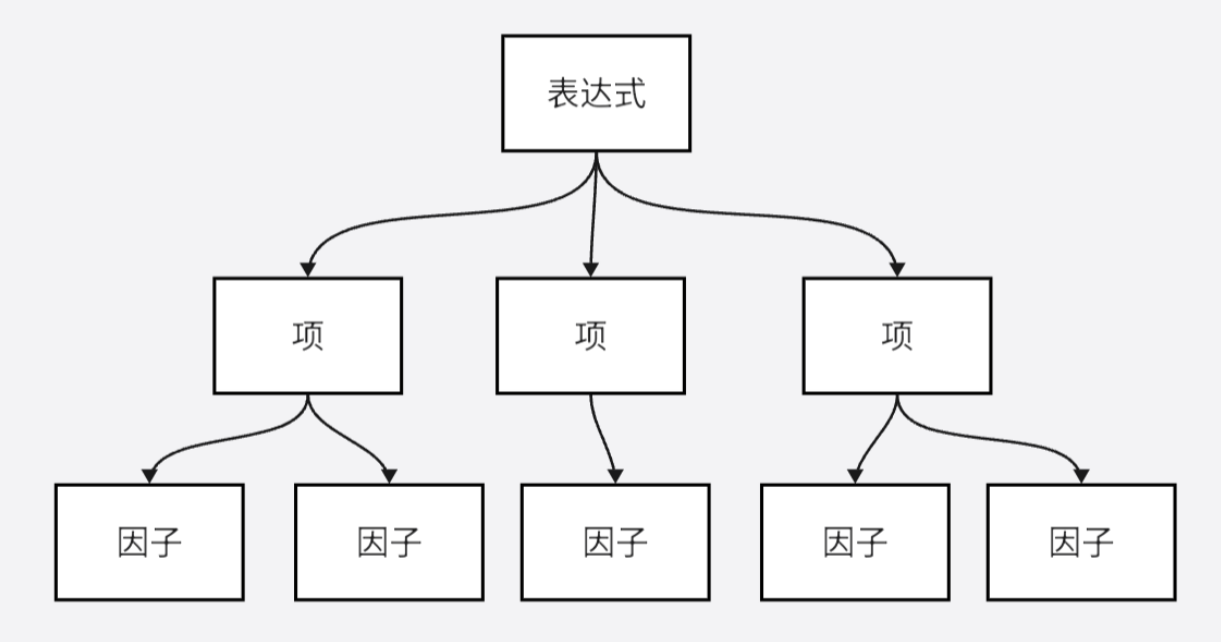
对于一个很复杂的表达式，我们该如何解析？

根据递归下降的思路，我们把表达式分为expr（表达式）、term（项）和factor（因子）。

  • term通过 ‘+’ 或 ‘-’ (不被括号包裹的加减号) 连接构成expr

    • 为了简化分割过程，我们可以把所有的 ‘-’ 替换为 ‘+-’，把 ‘-’ 看作项的一部分，从而可以只根据 ‘+’ (不被括号包裹的加号)分割 。

  • factor通过 ‘*’ (不被括号包裹的乘号) 连接构成term。

上述两个基本原则是我们解析表达式的关键，基于这两个原则我们可以从expr中提取若干term，从term中提取若干factor。

笔者舍弃了传统的Lexer和Parser，我认为解析Expr的方法就应该在Expr类里，在new一个Expr的实例的时候就提取出表达式里的term，构成一个ArrayList<Term>作为该Expr实例的一个属性。同理，在new一个Term的实例时候就提取出项里的factor，构成一个ArrayList<Factor>作为该Term实例的一个属性。

  •  1
 2
 3
 4
 5
 6
 7
 8
 9
10

    public class Expr {
    private ArrayList<Term> terms = new ArrayList<>();

    public Expr(String expr) {
        terms = extractTerms();
        ...
    }

	public ArrayList<Term> extractTerms() {...}
}

  •  1
 2
 3
 4
 5
 6
 7
 8
 9
10

    public class Term {
    private ArrayList<Factor> factors = new ArrayList<>();

    public Term(String term) {
        this.factors = extractFactors();
        ...
    }

	private ArrayList<Factor> extractFactors() {...}
}

image7-1

因子有好多类型，该如何处理？

使用抽象类+工厂模式

各类因子（ExprFactor、powFactor等等）继承抽象类Factor，这样Term里的存储因子的ArrayList<Factor>就可以存储各类因子了。

但是我们在new一个Factor的时候是不知道这个Factor的类型的，而不同因子又有不同的方法和属性，所以我们需要一个工厂，我们传入一个因子的字符串，工厂为我们提供对应类型的因子。

至于如何判断因子的种类，我采用的是正则匹配的方法，指导书中给出了明确的形式化表述，所以我们根据其要求构造正则表达式即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public class FactorFactory {
	public static Factor getFactor(String s) {
        ...
    	if (constRe.matcher(s).matches()) {
            return new ConstFactor(s);
        } else if (powerRe.matcher(s).matches()) {
            return new PowerFactor(s);
        } else if (sinRe.matcher(s).matches() || cosRe.matcher(s).matches()) {
            return new SinCosFactor(s);
        } else if (recursiveFuncRe.matcher(s).matches()) {
            return new RecursiveFuncFactor(s);
        } else {
            ...
        }
    }
}

在得到了表达式树之后如何化简？

用我们小学二年级就学到的思路，把每个因子都化成单项式，然后合并同类项。

在第二次作业添加了三角函数之后，表达式化简后的最小不可分单元不再是单项式，需要重新定义最小单元：AtomElement。

∑(coe∗xpow∗∏sin(factor)pow∏cos(factor)pow) \sum (coe*x^{pow}*\prod sin(factor)^{pow}\prod cos(factor)^{pow}) 
1
2
3
4
5
6
7

public class AtomicElement {
	private BigInteger coe;
    private final int xPow;
    private final int yPow;
    private final ArrayList<SinCosFactor> triFactors = new ArrayList<>();
    ...
}
  • 为什么BigInteger没有用final修饰，因为coe系数会有取相反数的操作。
  • 为什么会有一个yPow，那是因为后续的函数定义解析过程中会出现y项，不过结果中不会出现y项。

定义了最小单元之后我们如何获得AtomElement呢？

为了规范和统一，我们定义一个接口，要求能被转化为AtomElement的类（Expr、Term、Factor）都必须实现一个获得ArrayList<AtomElement>的方法。

我们规定Expr/Term/Factor等价于对应getAtomicElement()得到的ArrayList<AtomElement>中的每个元素相加。

expr的getAtomicElements()方法需要调用其包含的每一个term的getAtomElements()方法，每一个term又需要调用其包含的每一个factor的getAtomElements()方法，然后一层层返回最终得到表达式expr包含的所有AtomElement，合并可以合并的AtomElement之后再把每一个AtomElement转化为字符串再用 ‘+’ 相连即得到最终的化简结果。

1
2
3

public interface AtomicArrayConvertible {
    ArrayList<AtomicElement> getAtomicElements();
}

求导该如何解决？

由于作业中规定求导因子的dx(…)括号内为一个表达式，我们可以仿照getAtomicElements()的思路，再定义一个Derivable接口，所有可导的东西都需要实现这个接口中的derive方法。

我们同样需要规定Expr/Term/Factor求导后的结果等价于对应derive()得到的ArrayList<AtomElement>中的每个元素相加。

遇到一个求导因子，我们获取其最外层括号内的内容，构造一个expr实例，然后调用这个expr的derive()方法，expr的derive()方法需要调用其包含的每一个term的derive()方法，每一个term又需要调用其包含的每一个factor的derive()方法，然后一层层返回最终得到表达式expr包含的所有AtomElement，合并可以合并的AtomElement之后再把每一个AtomElement转化为字符串再用 ‘+’ 相连即得到最终的求导结果。

需要注意，求导因子也需要实现derive方法，即可以对一个求导因子再求导。

1
2
3

public interface Derivable {
    ArrayList<AtomicElement> derive();
}

递归函数该如何解决？

由于指导书限制了每次最多只会定义一个递归函数，所以我们可以再递归函数因子下用一个static类型的HashMap存储递归函数的三条定义（f{0}, f{1}, f{n}），key为函数的序号，value为’=‘后的函数表达式。至于形参我们再用一个static类型的ArrayList<String>来存，因为在一个递归函数定义中形参都是一样的。

在输入递归函数定义时，我们把定义存入HashMap中。在遇到递归函数因子时，我们先判断其序号是否在map中

  • 如果map中有对应的序号key，则直接把对应的value（函数表达式）取出，将形参替换为实参后构造一个Expr类型的实例，然后利用Expr的getAtomicElement()得到化简结果返回即可。
  • 如果map中没有对应的序号key，这是需要根据f{n}的规则进行递归解析，把n-1和n-2替换为对应的序号，再传入实参得到一个改造后的字符串，利用这个字符串构造Expr，调用Expr的getAtomicElements()即可得到结果。

普通函数呢？

大致思路和递归函数一样，都是字符串替换后再解析的思路。但是需要注意的是，作业中规定普通函数定义最多有两个，这两个函数的形参可能不一样，我们可以用一个static类型的HashMap<String, ArrayList<String>>存储每个函数对应的形参，其中key是函数名g或者h，value是形参的list。

在递归函数和普通函数用实参替换形参的过程中都涉及到一个问题，那就是第一个形参的替换不能影响第二个形参的替换，举个例子

f{1}(x,y) = x + y

f{1}(y,x)应该等于y + x，而遍历替换的时候会出现下述情况

(1) f{1}(y,x) = y + y (x被替换为实参y)

(2) f{1}(y,x) = x + x (y被替换为实参x)

我们可以引入一个中间量z来解决这个问题

(1) f{1}(x,z) = x + z (变换函数定义，第二个形参y替换为中间量z)

(2) f{1}(y,x) = y + z (把第一个形参x都替换为实参y)

(3) f{1}(y,x) = y + x (把第二个形参z都替换为实参x)

因为理论上两个形参应该是同时被替换的，但是在实现过程中这样并不可信，我们只能通过遍历的方式去替换，但最终要做到同时替换的效果，具体实现代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

private String replaceParam(String s, ArrayList<String> actualParamList) {
    int idx = 0;
    String secondParam = "";
    String result = s;
    if (formalParamList.size() > 1) {
        secondParam = formalParamList.get(1);
        result = result.replaceAll(secondParam, "z");
        formalParamList.set(1, "z");
    }
    // 代入实参
    for (String param: formalParamList) { 
        result = result.replaceAll(param, "(" + actualParamList.get(idx) + ")");
        idx++;
    }
    result = result.replaceAll("z", secondParam);
    if (formalParamList.size() > 1) {
        formalParamList.set(1, secondParam);
    }
    return result;
}

至此，整个框架已经搭建好了，我们只需要根据前面的规定实现对应的函数功能即可。

新增迭代场景展望

新增自定义变量因子，原变量因子之可能出现变量’x’，不妨让用户自定义变量名和变量数

1
2
3
4
5
6
7
8
9

example input:
3
a
b
var
a^3 + a*(var + a)^2 + sin(a^3-b-a^3)^2

expected output:
2*a^3 + 2*var*a^2 + var^2*a + sin(b)^2

在这个新场景中，需要

  • 修改term提取factor的规则
  • 修改FactorFactory中关于变量因子的正则表达式
  • 新增AtomicElement的属性，每个变量的幂次
  • 修改合并同类相的逻辑

优化分析

CTLE

在处理复杂结构时会出现超时的情况，通过添加cache缓存可以加快程序的运行速度。

所谓缓存就是把已经计算出的结果储存起来，再次使用的时候不需要重复计算，直接取出之前的结果即可。

  • 需要确保缓存的内容不会被修改，如果必须被修改则缓存也需要被修改。
  • 因为未改动程序的逻辑，所以并不会影响程序的正确性。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public class Expr implements AtomicArrayConvertible, Derivable {
    private ArrayList<AtomicElement> cachedAtoms = new ArrayList<>();
    ...
	@Override
    public ArrayList<AtomicElement> getAtomicElements() {
        if (!cachedAtoms.isEmpty()) {
            return cachedAtoms;
        }
        
        /*process of getting atoms*/
        
        cachedAtoms = atoms;
        return cachedAtoms;
    }
    ...
}

MLE / OOM

利用Eclipse Memory Analyse Tools分析Java堆，排查OutOfMemory (OOM)的问题。

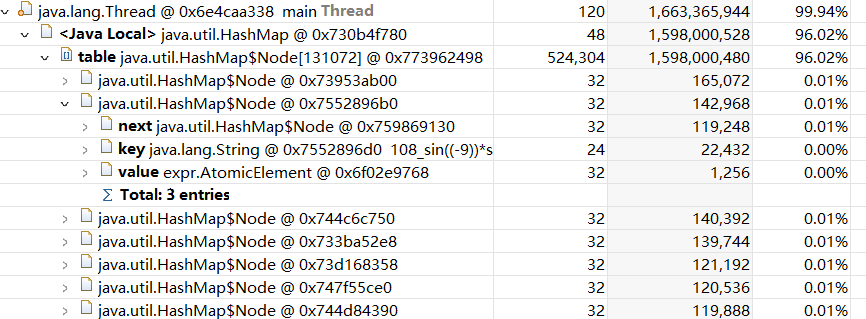
屏幕截图 2025-03-17 000230

把未化简的字符串当成了map的key，且合并同类项的逻辑有问题，导致HashMap中存在大量的键值对，把字符串化简之后再当作key并优化化简逻辑之后轻松解决OOM的问题。

  • 只需要确保优化前后结果的等价性即不会影响程序的正确性。

程序度量分析

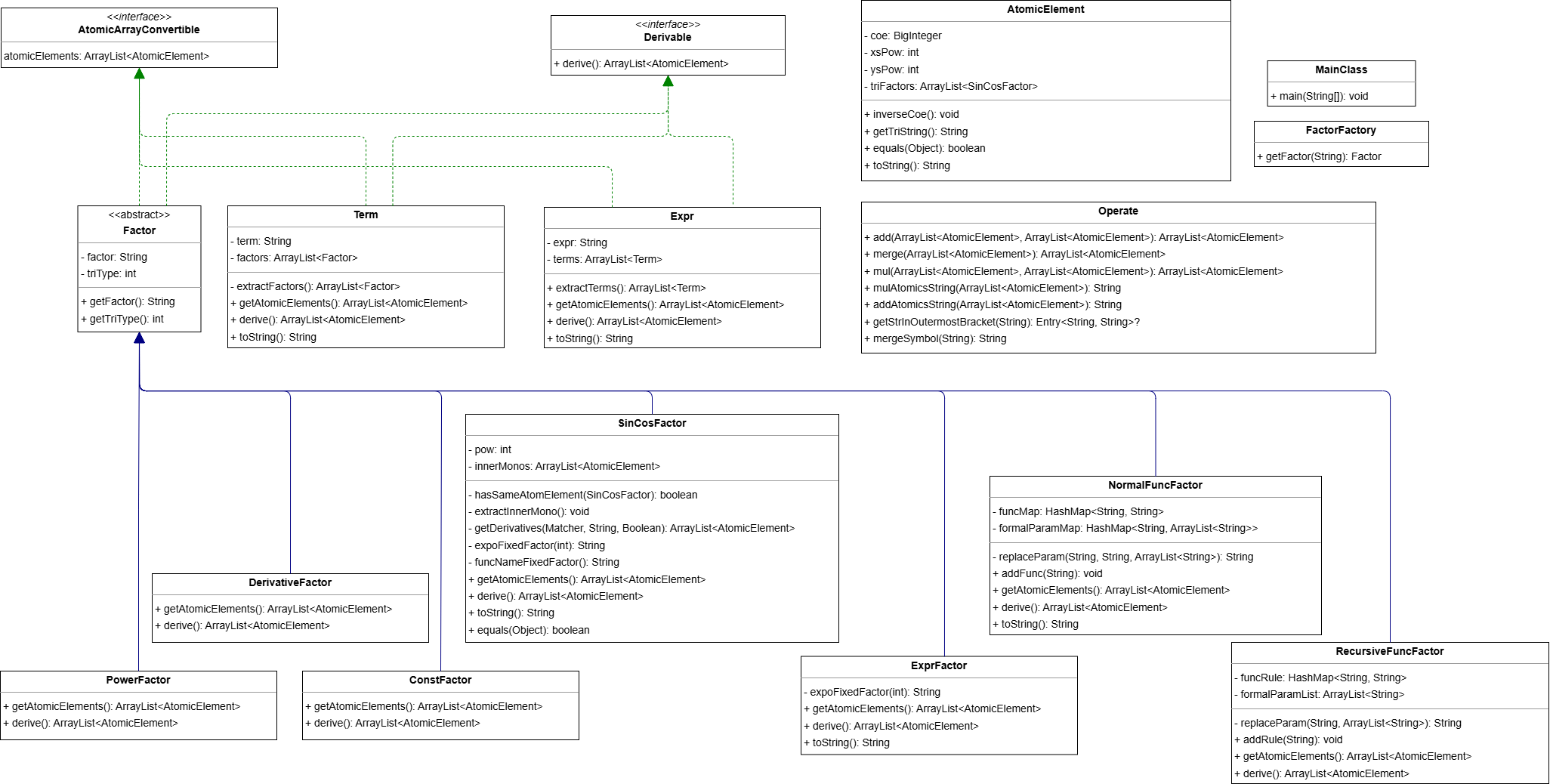
UML

exported_from_idea.drawio (1)

代码行数

屏幕截图 2025-03-19 153904

  • 从代码量可以看出，最复杂的部分应该就是三角函数，因为三角函数因子无论是解析还是化简求导都是所有因子中最复杂的。

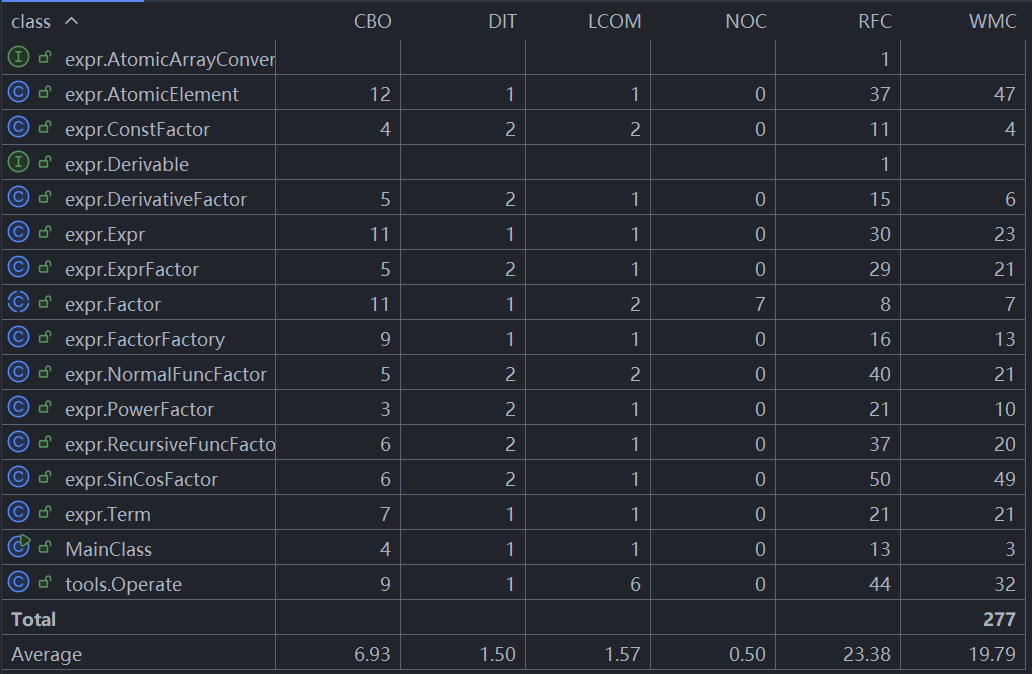
类的分析

  • CBO (Coupling Between Objects 对象耦合度) = 6.93 中等耦合，可接受
  • LCOM (Lack of Cohesion of Methods 方法内聚性缺失) = 1.57 低内聚，类可能需要拆分
  • 显然本次本次作业并没有很好的实现"高内聚低耦合"的理想设计目标。

屏幕截图 2025-03-19 154458

方法复杂度

  • 复杂度过高的方法一般都是字符串处理或者获取特定ArrayList，这主要是因为这两种情况处理比较复杂，有许多需要特判的情况，使用了大量的if-else语句。

PixPin_2025-03-19_22-36-21

自己的bug

  • 双形参函数在替换实参的过程中，第一个形参的替换影响了第二个形参的替换。具体原因在思路介绍的时候已经提出了，通过引入一个中间量z解决。
  • 获取函数形参的时候仅通过 ‘,’ 来分割，在遇到形如f{2}( f{1}(x,y), x)的因子时会解析错误，解决方法是在最外层括号内部遇到 ‘,’ 时判断一下是否被括号所包裹，如果不被包裹则分割获得形参。
  • 求导因子内部的derive()方法思路错误，这个方法应该是对求导因子再求导，而不是返回求导因子的结果，导致无法处理嵌套求导。修复derive()方法的逻辑即可。

出现这些bug的主要原因是写代码时没有全面的考虑可能出现的情况，想到什么就写什么，后续也没有进行充分的测试。可以通过编写测试单元、构造多样数据进行充分测试尽可能避免类似的bug。

如何发现别人程序bug

  • 评测机随机大量数据测试
  • 找到错误后查看源代码定位问题
  • 针对特定问题想出较为简单的测试数据提交hack
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

# hw2数据生成代码思路
class DataMakerH2:
    # 生成一个随机幂
    def _rand_power(self, isY):
    # 生成一个随机表达式因子
    def _rand_expr_factor(self, isY, hasRecursiveFactor, formal_param):
    # 生成一个随机三角函数因子
    def _rand_sin_cos(self, isY, hasRecursiveFactor, formal_param):
    # 生成一个随机因子
    def _rand_factor(self, isY, hasRecursiveFactor=False, formal_param=""):
        rand = random.random()
        if rand < 0.2 and self.inBrackets < 3:
            return self._rand_expr_factor(isY, hasRecursiveFactor, formal_param)
        elif rand < 0.4 and hasRecursiveFactor:
            return self._rand_recursive_factor(formal_param)
        elif rand < 0.6:
            return self._rand_signed_int()
        elif rand < 0.8 and self.inBrackets < 3:
            return self._rand_sin_cos(isY, hasRecursiveFactor, formal_param)
        else:
            return self._rand_power(isY)
    # 生成一个随机项
    def _rand_term(self, isY, hasRecursiveFactor, formal_param):
    # 生成一个随机表达式
    def _rand_expr(self, isY, hasRecursiveFactor, formal_param):
    # 生成一个单独的表达式
    def _generate_single_expr(self, isY ,hasRecursiveFactor, formal_param):
    # 生成f{0}和f{1}的表达式
    def _rand_func_expr(self, formal_param):
        if formal_param == "x,y" or formal_param == "y,x":
            func_expr = self._rand_expr(isY=True, hasRecursiveFactor=False, formal_param=formal_param)
            if random.random() < 0.5:
                func_expr += self._rand_expr(isY=False, hasRecursiveFactor=False, formal_param=formal_param)
        elif formal_param == "y":
            func_expr = self._rand_expr(isY = True, hasRecursiveFactor=False, formal_param=formal_param)
        else:
            func_expr = self._rand_expr(isY = False, hasRecursiveFactor=False, formal_param=formal_param)
        return func_expr
    # 生成f{n}的表达式
    def _rand_recursive_func_expr(self, formal_param):
        if formal_param == "x,y" or formal_param == "y,x":
            sub1_expr = str(random.randint(-10, 10)) + "*f{n-1}" + "(" + self._rand_factor(isY=False) + ", " + self._rand_factor(isY = True) + ")"
            sub2_expr = str(random.randint(-10, 10)) + "*f{n-2}" + "(" + self._rand_factor(isY=False) + ", " + self._rand_factor(isY = True) + ")"
        elif formal_param == "x":
            sub1_expr = str(random.randint(-10, 10)) + "*f{n-1}" + "(" + self._rand_factor(isY=False) + ")"
            sub2_expr = str(random.randint(-10, 10)) + "*f{n-2}" + "(" + self._rand_factor(isY=False) + ")"
        else:
            sub1_expr = str(random.randint(-10, 10)) + "*f{n-1}" + "(" + self._rand_factor(isY = True) + ")"
            sub2_expr = str(random.randint(-10, 10)) + "*f{n-2}" + "(" + self._rand_factor(isY = True) + ")"
        return sub1_expr + "+" + sub2_expr
    # 生成一个随机递归规则
    def _rand_recursive_rule(self, formal_param):
    # 生成一个随机递归函数因子
    def _rand_recursive_factor(self, formal_param):
    # 生成一个包含递归函数的测试点
	def _rand_recursive_example(self):

心得体会

  • 对面向对象的思想（封装、继承和多态）有了更深层次的理解，能够在实际编码中合理运用，例如通过封装提高代码的模块化，通过继承实现代码复用，以及通过多态增强系统的扩展性和灵活性。
  • 对工厂模式的理解更加深入，能够在合适的场景下运用工厂模式来解耦对象的创建过程，提高代码的可维护性和可扩展性，从而实现更灵活的设计。
  • 在不断迭代的过程中认识到了规范的重要性，遵循一些设计规范和命名规则，不但能提高效率，还能减少错误。
  • 通过不断的迭代和小范围重构，深刻认识到了程序可扩展性的重要性，写代码时不仅要考虑当下的要求，还需要考虑后续可能会有哪些新的要求。
  • 通过自己编写评测机，对数据生成的流程和方法有了更全面的认识，深入理解了如何设计高效的数据生成策略，以确保测试数据的多样性和合理性。
  • 真切感受到了自己代码能力的提高。

未来方向

  • 希望能简化一些限制，指导书写的简洁明了一点，减少学生在阅读指导书上花的时间，把更多的精力放在代码设计上。
© 2020 - 2025 Az's Blog
使用 Hugo 构建
主题 Stack 由 Jimmy 设计